KALKULUS bahasa Latin: calculus, artinya "batu kecil", (untuk menghitung) adalah cabang ilmu matematika yang mencakup limit, turunan, integral, dan deret takterhingga. Kalkulus memiliki aplikasi yang luas dalam bidang-bidang sains, ekonomi, dan teknik; serta dapat memecahkan berbagai masalah yang tidak dapat dipecahkan dengan aljabar elementer.
Pelajaran kalkulus adalah pintu gerbang menuju pelajaran matematika lainnya yang lebih tinggi, yang khusus mempelajari fungsi dan limit, yang secara umum dinamakan analisis matematika.
PRINSIP-PRINSIP DASAR
A. Limit
Limit menjelaskan nilai suatu fungsi pada nilai input tertentu dengan hasil dari nilai input terdekat. Dari sudut pandang ini, kalkulus adalah sekumpulan teknik memanipulasi limit-limit tertentu. Maksudnya gini *saya usahakan menjelaskan sebisa saya* Limit adalah bahasa Inggris yang artinya "menuju". Misalnya limit menuju 0. Kita gabisa bilang itu adalah 0, tapi "menuju". Sehingga kalo 1/2, 1/3, bahkan 1/10000000 pun adalah menuju 0 :D
B. Turunan
Turunan dari suatu fungsi mewakili perubahan yang sangat kecil dari fungsi tersebut terhadap variabelnya. Proses menemukan turunan dari suatu fungsi disebut sebagai pendiferensialan ataupun diferensiasi.
C. Notasi Pendiferensian
Notasi Leibniz diperkenalkan oleh Gottfried Leibniz. Turunan dari fungsi tersebut terhadap x ditulis sebagai:
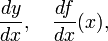 ataupun
ataupun 
Notasi Newton, juga disebut sebagai notasi titik, menempatkan titik di atas fungsi untuk menandakan turunan. Apabila y = ƒ(t), maka 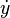 mewakili turunan y terhadap t. Notasi ini digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika.
mewakili turunan y terhadap t. Notasi ini digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika.
Notasi Lagrange diperkenalkan oleh Joseph Louis Lagrange dan merupakan notasi yang paling sering digunakan. Dalam notasi ini, turunan fungsi ƒ(x) ditulis sebagai ƒ′(x) ataupun hanya ƒ′.
Notasi Euler menggunakan operator diferensial D yang diterapkan pada fungsi ƒ untuk memberikan turunan pertamanya Df. Apabila y = ƒ(x) adalah variabel terikat, maka sering kali x dilekatkan pada D untuk mengklarifikasikan keterbebasan variabel x.
D. INTEGRAL
Integral merupakan suatu objek matematika yang dapat diinterpretasikan sebagai luas wilayah ataupun generalisasi suatu wilayah. Proses menemukan integral suatu fungsi disebut sebagai pengintegralan ataupun integrasi. Integral dibagi menjadi dua, yaitu: integral tertentu dan integral tak tentu. Notasi matematika yang digunakan untuk menyatakan integral adalah  , seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan).
, seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan).
Saya yakin untuk integral kalian sudah tahu maksud mendalamnya. Integral dibagi dua yaitu intergral tentu dan integral tak tentu. Yang tentu, kalo kalian masih inget pas kelas 3 SMA, kan integral yang tentu itu yang punya batas. Nah kalo yang tak tentu itu yang ga ada batasnya
Source : http://id.wikipedia.org/wiki/Kalkulus
Baiklah hanya sekian yang bisa saya share mengenai kalkulus I. Ternyata jujur aja saya baru sadar kalo pas kita SMA, kita udah belajar dasar kalkulus :) Thanks for reading, comment please #ehem



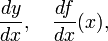 ataupun
ataupun 
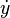 mewakili turunan y terhadap t. Notasi ini digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika.
mewakili turunan y terhadap t. Notasi ini digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika. , seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan).
, seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan).